Вычисление суммы - это математическая операция сложения двух или более чисел, результатом которой является общее значение, называемое суммой. Это одна из четырех основных арифметических операций.
Содержание
Основное определение
Вычисление суммы - это математическая операция сложения двух или более чисел, результатом которой является общее значение, называемое суммой. Это одна из четырех основных арифметических операций.
Основные принципы сложения
| Принцип | Описание |
| Коммутативность | a + b = b + a (порядок слагаемых не влияет на сумму) |
| Ассоциативность | (a + b) + c = a + (b + c) (группировка слагаемых не влияет на результат) |
| Существование нуля | a + 0 = a (нуль является нейтральным элементом сложения) |
Виды сумм
- Алгебраическая сумма (включает положительные и отрицательные числа)
- Арифметическая сумма (только положительные числа)
- Накопленная сумма (результат последовательного сложения)
- Взвешенная сумма (с учетом коэффициентов важности)
Обозначение суммы в математике
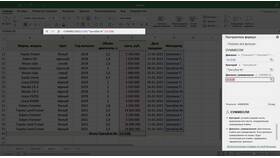
В математике сумма часто обозначается греческой буквой Σ (сигма):
Σ (от i=1 до n) ai = a1 + a2 + ... + an
Методы вычисления сумм
- Последовательное сложение (пошаговое прибавление чисел)
- Использование свойств сложения (группировка удобных слагаемых)
- Применение формул (для арифметических и геометрических прогрессий)
- Использование вычислительной техники (калькуляторы, компьютеры)
Примеры вычисления сумм
| Пример | Вычисление | Результат |
| Простые числа | 3 + 5 | 8 |
| Несколько слагаемых | 2 + 4 + 6 | 12 |
| С отрицательными числами | 7 + (-3) | 4 |
Применение вычисления сумм
- Финансовые расчеты (подсчет доходов, расходов)
- Статистика (вычисление итоговых показателей)
- Программирование (агрегация данных)
- Физика (суммирование сил, энергий)
- Бухгалтерия (подведение баланса)
Особые случаи
В некоторых областях используются специфические виды сумм:
- Контрольные суммы (в информатике)
- Векторные суммы (в физике)
- Интегральные суммы (в высшей математике)
- Ряды (бесконечные суммы)
