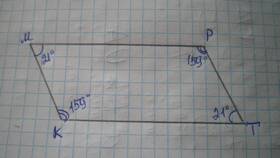
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. Рассмотрим свойства его углов и методы вычисления их суммы.
Содержание
Основные свойства углов параллелограмма
- Противоположные углы равны
- Сумма соседних углов составляет 180°
- Все внутренние углы в сумме дают 360°
- Диагонали делят углы пополам
Доказательство суммы углов
- Проведите одну из диагоналей параллелограмма
- Диагональ разделяет фигуру на два равных треугольника
- Сумма углов каждого треугольника равна 180°
- Таким образом, сумма углов параллелограмма: 180° × 2 = 360°
Графическое представление
| Угол A | Угол B | Угол C | Угол D |
| α | 180° - α | α | 180° - α |
Практические примеры расчета
| Пример | Решение |
| Один угол равен 60° | Противоположный: 60°, соседние: 120° |
| Разность двух углов 40° | Углы: 110° и 70° (так как 110° - 70° = 40°) |
Алгоритм нахождения отдельных углов
- Обозначьте один угол как x
- Соседний угол будет 180° - x
- Противоположные углы равны обозначенному
- Составьте уравнение по условию задачи
- Решите уравнение и найдите все углы
Применение свойств в задачах
- При расчете площадей параллелограмма
- В задачах на построение геометрических фигур
- При доказательстве равенства треугольников
- В векторной алгебре и физических расчетах
Важное замечание
Сумма внешних углов параллелограмма, взятых по одному при каждой вершине, также равна 360°. Каждый внешний угол смежен с внутренним и равен 180° минус величина внутреннего угла.