Сумма углов трапеции, как и любого другого четырёхугольника, составляет 360 градусов. Это фундаментальное свойство евклидовой геометрии, которое следует из того, что трапеция является частным случаем четырёхугольника.
Содержание
Доказательство суммы углов трапеции
Общее свойство четырёхугольников
Любой четырёхугольник можно разделить на два треугольника диагональю. Поскольку сумма углов треугольника равна 180 градусов, то сумма углов четырёхугольника составляет 180° × 2 = 360°.
Частный случай трапеции
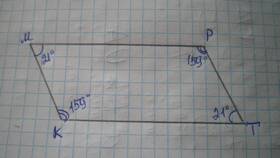
Трапеция - это четырёхугольник, у которого две стороны параллельны (основания), а две другие - непараллельны (боковые стороны). Несмотря на эту особенность, общая сумма углов остаётся равной 360 градусам.
| Тип углов | Количество | Свойства |
| Углы при одном основании | 2 | Дают в сумме 180° |
| Углы при другом основании | 2 | Также дают в сумме 180° |
| Все углы трапеции | 4 | Сумма 360° |
Особенности углов трапеции
Углы при боковой стороне
Углы, прилежащие к одной боковой стороне, являются односторонними и в сумме дают 180 градусов.
Равнобедренная трапеция
В равнобедренной трапеции углы при каждом основании равны между собой:
- ∠A = ∠D
- ∠B = ∠C
- ∠A + ∠B = 180°
- ∠C + ∠D = 180°
Прямоугольная трапеция
У прямоугольной трапеции два угла являются прямыми (по 90 градусов), а сумма оставшихся двух углов также составляет 180 градусов.
Примеры расчётов
- Если три угла трапеции равны 80°, 100° и 70°, то четвёртый угол равен: 360° - (80° + 100° + 70°) = 110°
- В равнобедренной трапеции с углами при основании 65°, другие два угла будут: 180° - 65° = 115° каждый
- В прямоугольной трапеции с одним прямым углом и вторым углом 75°, остальные углы будут 90° и 105°
Важные замечания
- Сумма углов трапеции не зависит от длины её сторон
- Это свойство верно для любых трапеций - произвольных, равнобедренных, прямоугольных
- В неевклидовой геометрии сумма углов четырёхугольника может отличаться от 360 градусов